RALLY SISTEMAS ESTRUCTURALES VI
CRUZ
MIRANDA VICTOR HUGO
JIMÉNEZ
HERNÁNDEZ SINDY ESTEFANÍA
VALENCIA
DURÁN PEDRO
RALLY SISTEMAS ESTRUCTURALES VI
1. EJE NEUTRO: CALCULO
Hipótesis
de Bernouilli – Navier: “ En la Flexión Pura cada sección transversal de la viga
gira alrededor de un eje, contenido en la sección, denominado Eje Neutro,
permaneciendo las secciones planas y normales a las fibras deformadas”.
Admitiremos
también que la flexión se produce en régimen elástico y por tanto dentro de los
límites de validez de la Ley de Hooke, por lo que las tensiones que se originan
han de ser proporcionales a las deformaciones producidas.
Al
flexionar la viga, las secciones transversales giran y hacen que las fibras longitudinales,
inicialmente rectas, dejen de serlo y se curven, alargándose o acortándose
según sea su posición en el interior de la viga.
Existen
fibras longitudinales que ni se alargan ni se acortan, a esas fibras se las
denomina
FIBRAS
NEUTRAS.
A la
superficie donde se encuentran las fibras neutras se la denomina SUPERFICIE NEUTRA.
Las fibras que estén por encima o por debajo de la Superficie Neutra alargarán
o acortarán según hacia donde flexione la viga. (En el caso del dibujo
acortarán las fibras que están por encima de la Superficie Neutra y alargarán
las que estén por debajo)
A las
fibras transversales de la Superficie Neutra se las denomina:
LINEAS
NEUTRAS o EJES NEUTROS. Alrededor de ellos giran las secciones transversales
En las
siguientes figuras se representan estos términos para su mejor identificación:
Así pues
como resultado de la flexión el paralelepípedo elemental abcd se transforma
en el a1b1c1d1 y como
según la Hipótesis de Bernouilli-Navier: “...... las secciones transversales de
la viga giran alrededor de un eje, contenido en la sección, denominado
Eje
Neutro, permaneciendo planas y normales a las fibras deformadas”, se deducirá
que: a1b1 será perpendicular a a1c1.
Con lo
cual se podrá afirmar: “Las deformaciones angulares de los diferentes paralelepípedos
son nulas, es decir: γ = 0”
CÁLCULO
DE LA LÍNEA NEUTRA (EJE NEUTRO)
Las
fibras que pertenecen a la Superficie Neutra, por definición, ni se alargan ni
se acortan, con lo cual se cumplirá:
Así pues
la ecuación de la línea neutra la podemos obtener como lugar geométrico de los
puntos de una sección que tienen tensión normal cero, es decir:
o lo que es lo mismo:
También
puede expresarse, sabiendo que ha de pasar por el centro de gravedad G de la
sección, en virtud de (5.6), por su ángulo de inclinación α con respecto al eje z.
2. CONSTANTES “J” Y “K”
J: es una
constante menor que la unidad que cambia su valor en función de la cuantía
empleada pero que puede ser estimada como un valor cercano a 0.9. Consideraremos
J = 0.89 para evitar que se confunda con el factor de reducción de resistencia.
K: Asociación de
Cemento Portland: De 0.9 a 1.0 (Para concretos de Alta a baja Resistencia,
respectivamente)
Reglamento de
Construcción del DF: 0.85
3.
PERALTE
EFECTIVO “d”
El Reglamento
especifica que el ancho de la viga no sea menor a 20cm, en consecuencia:
d2= Mu
FRf´c b y (1-0.59y)
4.
RELACION
V y M PARA SECCIONES:
Relación de
carga fuerza cortante y momento flector
La carga se
relaciona con la fuerza cortante y el momento flector, las cuales permiten un
método alternativo para dibujar los diagramas. Las relaciones están indicadas
en la Ecuación 3 (Popov,1996; Singer y Pytel, 1982).
5.
(As) EN BASE A QUE SE DETERMINA:
Las Normas
Técnicas Complementarias establecen que la sección debe alcanzar su resistencia
en forma dúctil, es decir, con grandes deflexiones que permitan al usuario
detectar la inminencia de la falla. Para ello, se obliga al diseñador a limitar
el área de acero tanto inferior como superiormente:
As min ≤ As ≤As max
En donde:
La expresión (7)
es aplicable a vigas que no deben resistir fuerzas sísmicas. En caso contrario,
el coeficiente mostrado equivale a 0.75 Para vigas que cumplen las ecuaciones 6
y 7 se pueden aplicar las siguientes expresiones para la obtención del momento
resistente MR:
MR = FR f"c b d2
q( 1-0.5q) (8)
MR = FR As fy d (1-0.5q) (9)
Donde:
MR= Momento
resistente de una sección
FR= Factor de
resistencia para flexión= 0.9
f ''c= Esfuerzo
uniforme en la hipótesis de Whitney (kg/cm2)
b,d= Base y
peralte efectivo de la sección (cm)
donde:
También
en este caso es obvio que la cuantía mínima de acero es calculada, partiendo de
la expresión (2.1) NTC como:
6.
REVISION
POR REGLAMENTO DE SECCION Y As
En
la práctica, existen tres tipos de problema:
A)
Problemas de revisión. En estos problemas se verifica que el momento resistente
MR
de la sección es mayor o cuando menos igual al momento último MU
B)
Problemas de dimensionamiento. En estos problemas solamente se conoce el
momento último que se desea resistir y las propiedades mecánicas de los
materiales (f’c y fy). Las incógnitas son las propiedades geométricas b, d y
AS.
C)
Problemas de armado. En este tipo de problemas se conoce el momento último MR,
las propiedades mecánicas de los materiales (f’c y fy) y las dimensiones b y d
.Solamente se tiene como incógnita el área de acero As.



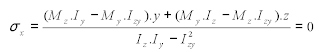







No hay comentarios:
Publicar un comentario